With the increasing scale of communication networks, failures (e.g. link failures) are becoming the norm rather than the exception. Given the critical role such networks play for our digital society, it is important to ensure a reliable and efficient operation of such networks, even in the presence of one or multiple failures. While several interesting automated approaches to verify and operate networks are emerging, offering an attractive alternative to today’s pragmatic and manual “fix it when it breaks” approach, existing solutions often only provide a limited and inefficient support for reasoning about failure scenarios. In particular, verifying networks is a complex task, even for computers. For example, many existing automated solutions require to test each possible failure scenario (respectively, each possible dataplane) individually, resulting in a runtime which can be exponential in the number of failures; which makes this approach impractical for large-scale communication networks. In fact, certain communication networks, such as networks based on MultiPath Label Switching (MPLS) or Segment Routing (SR), may even have a theoretically infinite configuration space: in MPLS and SR networks, default routes as well as failover routes depend on the label stack in the packet header, which may grow and shrink arbitrarily along the route.
In this article, we argue that automata-theoretic approaches can offer an interesting solution to these problems, allowing to perform fast verification, accounting even for failure scenarios and dealing with potentially infinite state spaces.
A case for verifying network configurations
Before delving into the details, we first argue that it is often attractive to verify the network configuration directly: compared to verifying control plane protocols, analyzing the dataplane configuration (e.g., forwarding and conditional failover tables) has the advantage that it also accounts for possible external changes, e.g., manual changes through the CLI, bugs, or changes made by additional protocols. Moreover, dataplane-based approaches can also reveal problems in the network operation introduced by the algorithms that generate the routing tables from the control plane specifications.
Let us consider the verification of forwarding rules in MPLS routing tables as an example. In a nutshell, in MPLS, packet labels can be nested in order to provide tunneling through the network or to handle link failures by the fast-reroute mechanism. This mechanism relies on pushing a new MPLS label on top of the label stack, to redirect the flow to go around the failed link. The mechanism can be applied several times in case of multiple link failures, creating larger and larger (in theory: unbounded) numbers of MPLS labels on the label-stack.
A fairly general query language which supports to reason about network behavior under failures could be based on regular expressions:
$ < a > b < c > k $
Here $a$ and $c$ are regular expressions over MPLS labels that describe the set of allowed initial resp. final headers of packets in the trace, $b$ is a regular expression over the links in the network, defining the set of allowed routing traces through the network, and $k$ is a number specifying the maximum number of failed links to be accounted for.
By using regular expressions, we can test properties such as waypoint enforcement (e.g., is the traffic always forwarded through an intrusion detection system) or avoidance of certain routers in selected countries.
How does polynomial-time what-if analysis work?
In order to evaluate such queries and conduct what-if analysis quickly, we make the case for a model-checking algorithm which is based on automata theory. Our approach is motivated by a natural (but not well-known) connection to the theory of pushdown automata and prefix rewriting systems. In a nutshell, given the network configuration, the routing tables, as well as the query, a pushdown automaton (PDA) can be constructed. On this PDA, we can then perform a standard reachability analysis. In more details, the regular expressions for the initial header and the final header of the query can each be converted to first a Nondeterministic Finite Automaton (NFA) and then to a Pushdown Automaton (PDA). The path query is converted to an NFA, which can then be used to restrict (by synchronous product) the behavior of the PDA constructed based on the network model. The three PDAs can be combined into a single PDA that can be given to the backend engine that checks the emptiness of the PDA language. In case the language is nonempty, we can return a witness trace to demonstrate the reason why the query is satisfied. All these operations can be performed in polynomial time, leveraging a classic result by J. Büchi.
The AalWiNes Tool and Example
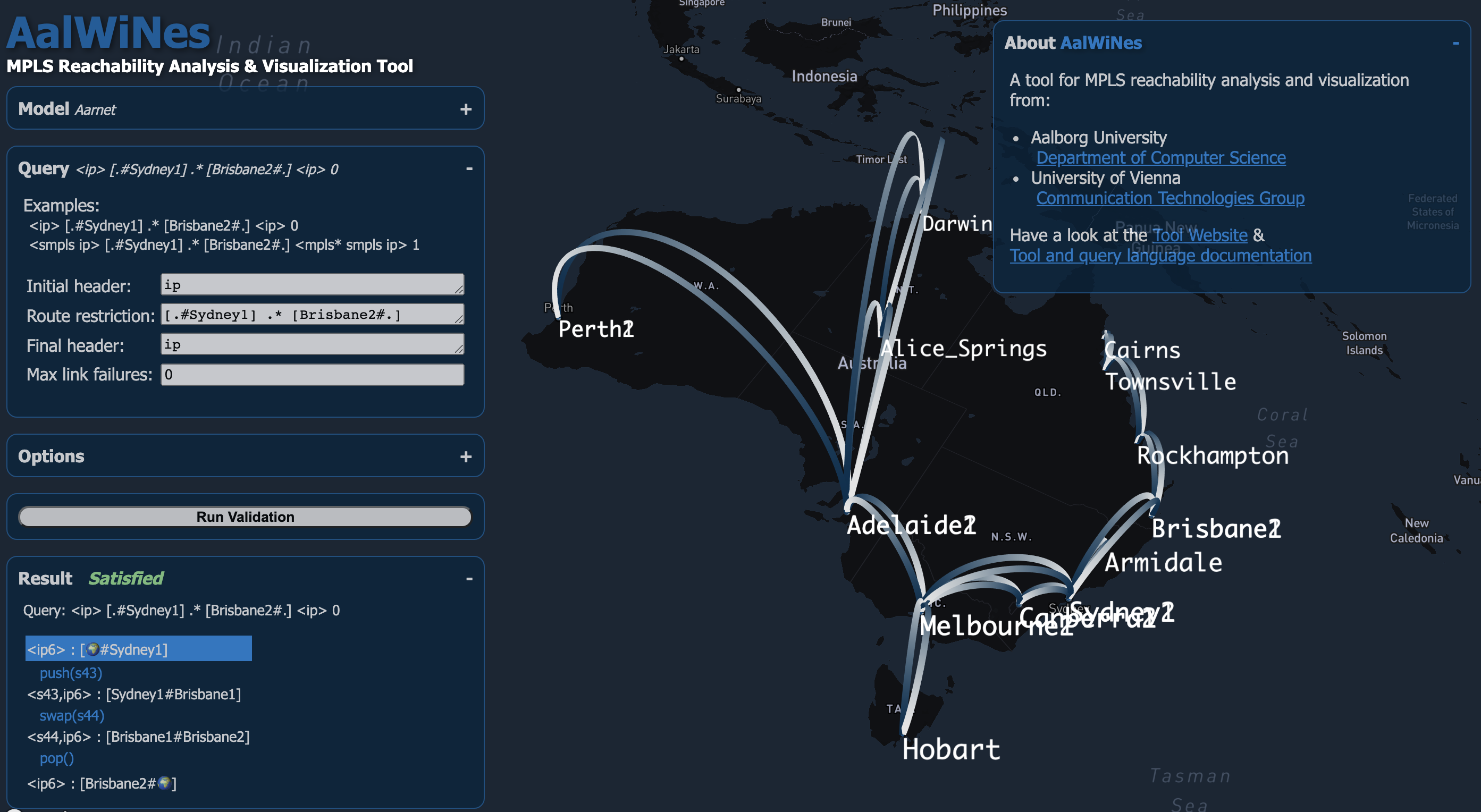
As a case study and to explore the feasibility of such an automata-theoretic approach, we developed a framework, the AalWiNes suite, which allows to load an arbitrary network topology (e.g., from the topology zoo dataset) as well as a set of router configurations (e.g., from Juniper routers). The configurations are put into a standardized, intermediate format which is vendor independent. The user can then define a query as described above, which leads the tool to prompt with a result (e.g. a trace). AalWiNes is a joint work at Aalborg University and the University of Vienna.
For MPLS specifically, we have devloped the AalWiNes tool suite, implemented in C++, and improving upon an earlier prototype implementation in Python [1]. The tool allows to verify a wide range of important network properties in polynomial time, parameterized by the $k$.
Here is a quick intro to AalWines, using an interative web-browser integration of our tool available at demo.aalwines.cs.aau.dk:
AalWiNes also allows to account for more complex traffic engineering aspects, such as load-balancing, by supporting nondeterminism, as well as more complex multi-operation chains. The tool includes several optimizations to further improve the performance, such as “top of stack reduction”, which safely calculates which labels can be at the top of stack in a given state of the PDA: the top of stack reduction technique greatly reduces the amount of transitions in the PDA.
We refer to our tool website as well as to our project website.
Conclusion and future work
Our aim is to provide a low runtime which is critical for the success of network verification, however, reasoning about failures seems particularly challenging with respect to the computational complexity. While not every network may allow for a polynomial-time analysis, we see much potential in automata-theoretic approaches, and we hope this article can inspire the community to conduct more research in this area.
We understand our approach as a first step and believe that it opens the door to verify many other infinite state systems whose configurations cannot explicitly be represented anymore. For example, we have recently extended AalWiNes to support a witness trace generation which accounts for additional metrics; for example, the tool can now select (among a possibly infinite number of witness traces) the ones that minimize the number of hops, latency, or the stack height that corresponds to the number of MPLS tunnels. This is achieved by extending the PDA reachability analysis with multi-dimensional weights.
Another interesting avenue for future research is the study of similar approaches for control plane verification or for supporting capacity planning, also taking into account resource constraints on failover paths.
References
[1] : P-Rex: Fast Verification of MPLS Networks with Multiple Link Failures. Jesper Stenbjerg Jensen, Troels Beck Krogh, Jonas Sand Madsen, Stefan Schmid, Jiri Srba, and Marc Tom Thorgersen. 14th ACM International Conference on emerging Networking EXperiments and Technologies (CoNEXT), Heraklion/Crete, Greece, December 2018.
 Stefan Schmid
Stefan Schmid  Jiri Srba
Jiri Srba